You’ve been hired for a job at a high-paying organization doing exactly what you want to do! Congratulations!
You start work in January, but you haven’t finalized the terms of your contract yet. Your new boss has given you the choice between two salary payment options to compensate you during your first year of work. Here they are:
Salary Option 1 $200,000 every month on the last day of the month.
Salary Option 2 You earn no money for the first 11 months of the year. On December 1st, you earn one penny. Your daily wage then doubles every day for 31 days in December.
Which choice earns you more money over the course of the year? Which option will you pick and why?
I gave my Algebra students a version of this problem — which I first saw while doing work with Dr. Jonathan Katz, whose book I highly recommend — to my class a few weeks ago as a performance task.
Clearly, option 1 is the best choice for the vast majority of the year. On December 2nd, option 1 has netted the fiction employee a total of $2.2 million while option 2 has only resulted in a penny. Even as late as December 21st, a day when our employee earns a not-too-shabby daily wage of more than $10,000, the total money she’s earned for the year is comparatively paltry — $20,971.51.
But as the daily wage gets bigger and bigger the change in wage per day also increases and increases and increases. The mathematical concept at play here is exponential growth. It creates a result which surprised most of my students.
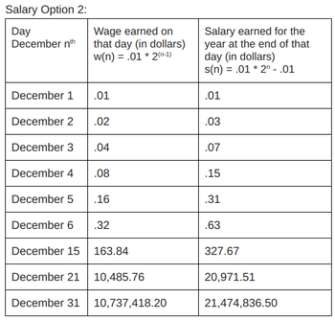
On New Year’s Eve our employee earns more than $10 million just for that one day, her yearly wage for option 2 is over $21 million, close to ten times the $2.4 million annual salary from option 1.
The idea of comparing a linear growth model (like the $200,000 per month) to an exponential is important and important in the Common Core. Using money to make a math performance task more engaging often seems like it works for my students. But the real beauty of this task is that it feels so surprising that option 2 ends up with a higher yearly salary given the relative difference of $200,000 and 1 penny.

The task utilizes a redirection by setting students up to intuit an incorrect solution at first glance. They then explore the context and realize that what was the “obvious solution” is not even close to the best choice.* Socrates used a similar method in teaching Meno, by having him first express is faulty intuition about a square’s area, then guiding him to the correct one.
Some of the lessons that stick with me the most from my own education are ones that changed my initial thinking. I used to think...but now I know... is a useful frame for developing learning sequences that will stick with students. Math teachers ought to look for situations where we can leverage the “aha” power of situations that conflict with our initial intuition.
What are some good problems that you use to make students think one thing in order to know something different?
*I’m defining “best choice” as the salary option that nets the employee the most money over the course of the year. Several students wrote about how they would rather earn more money up front, which I recognized as a valid solution strategy (especially for students who are used to budgeting month to month, not year to year) as along as they acknowledged that the larger yearly salary came from option 2. Something I talked with these students about was that if they select option 2 then they could theoretically borrow a lump sum (say $2.4 million) at the beginning of the year and pay it back with interest. The salary option 2 is so much larger that even with the added cost of financing this debt they would end up coming out ahead.
Photo 1: Plato from Rafael’s The School of Athens. In Meno Plato wrote about how Socrates utlized a common misconception about the area of a square to teach a young man about the real relationship between side lengths and area. Public Domain, https://commons.wikimedia.org/w/index.php?curid=884405
Photo 2: A table of Salary Option 2 (described above) by author.


